Research activities
We study interactions of electromagnetic radiation with condensed matter in a broad frequency range between static regime and visible light. This is obtained using a combination of several experimental techniques. Depending on the specific frequency range, different excitations can be observed and studied: phonons, magnons, magnetoelectric excitations, relaxation processes. Due to fundamental relation between static and dynamic properties, the observed features in the spectra are directly connected to such static properties like magnetisation, dielectric constant, or static electric polarization. Details of underlying microscopic mechanisms are extracted from magnetic and electric dispersion and absorption phenomena. Broadband optical spectroscopy is therefore a powerful method to reveal fundamental properties of condensed matter such as quantum Hall effect, charge dynamics at the metal-insulator transition, electron spin resonance, magnetoelectric effect, negative refraction in metamaterials, etc.
Experimental techniques
In the low frequency range (ν < 1 MHz) the sample in form of a capacitor is investigated.
The LRC analyzer obtains the amplitude and phase shift of the current through the sample.
The sample capacitance C which is proportional to the dielectric permittivity ε1+iε2 is obtained from
the complex impedance as C= 1/iωZ. This method is called Dielectric Spectroscopy.
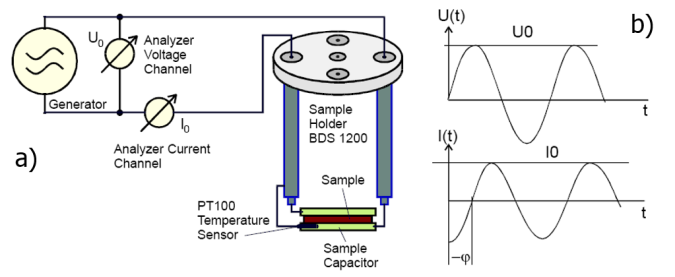
Fig. a) Principle of dielectric measurement [Novocontrol GmbH] and b) Amplitude and phase shift between ac voltage, U0sinωt, and ac current, I0sin(ωt+φ), through the
sample.
At higher frequencies (1 MHz < ν < 10 GHz) the cable effects are getting important.
Therefore, the sample is placed as an end-element of the coaxial cable.
The reflectance (r) in the cable is measured and it is given by:
r=(Z-Z0)/(Z+Z0)
Here Z = 1/ iωC is the complex impedance of the sample, and Z0 = 50 Ω is the wave-impedance of the cable.
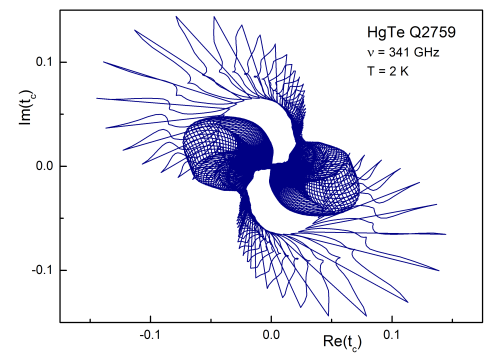
In the terahertz frequency range a BWO-type spectrometer is used, which
allows measurement of the complex transmission and reflection coefficients
as a function of external parameters like magnetic fields or temperature.
Using Fresnel optical equations permittivity, conductivity or refractive index
is obtained without additional assumptions.
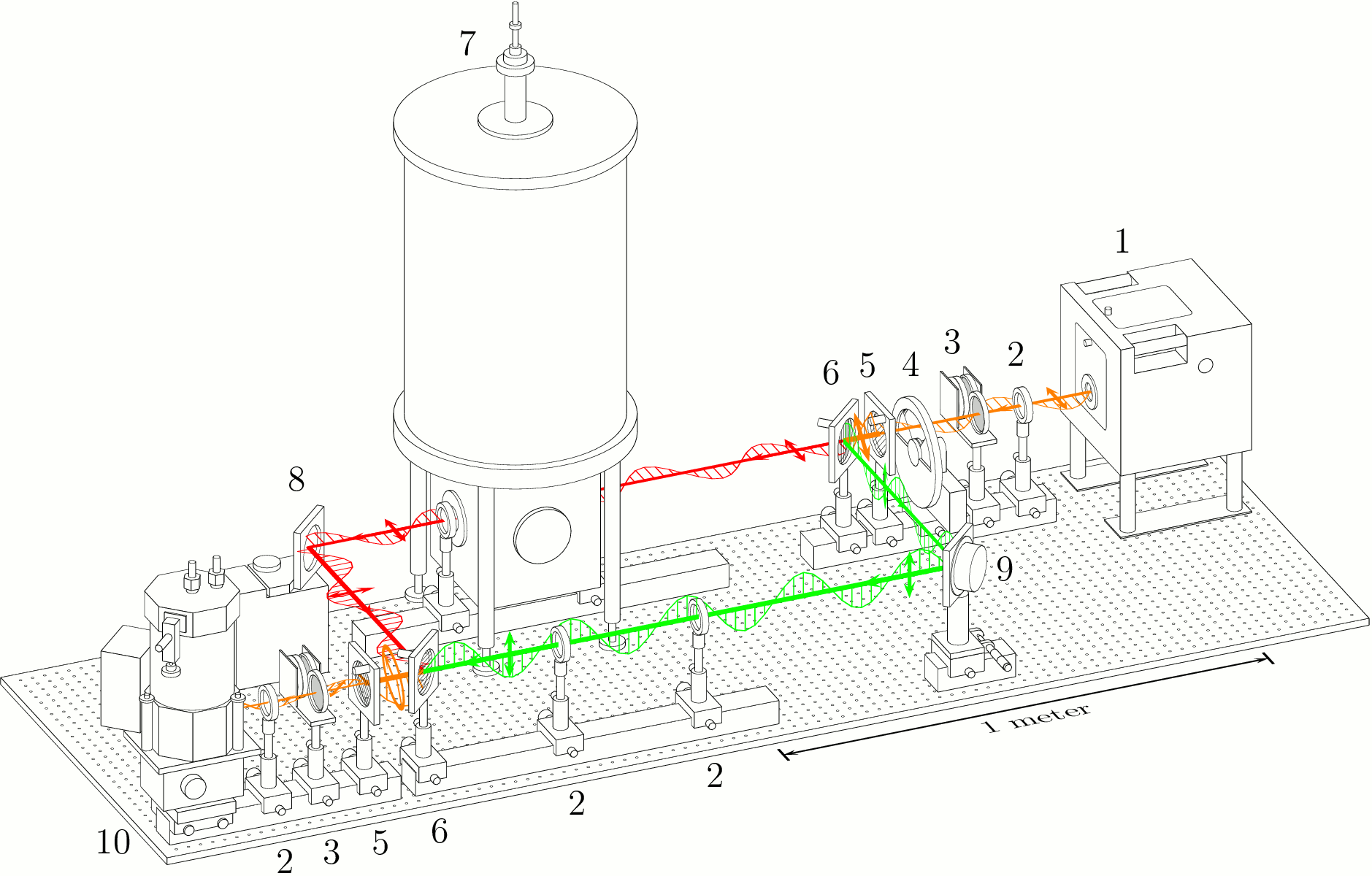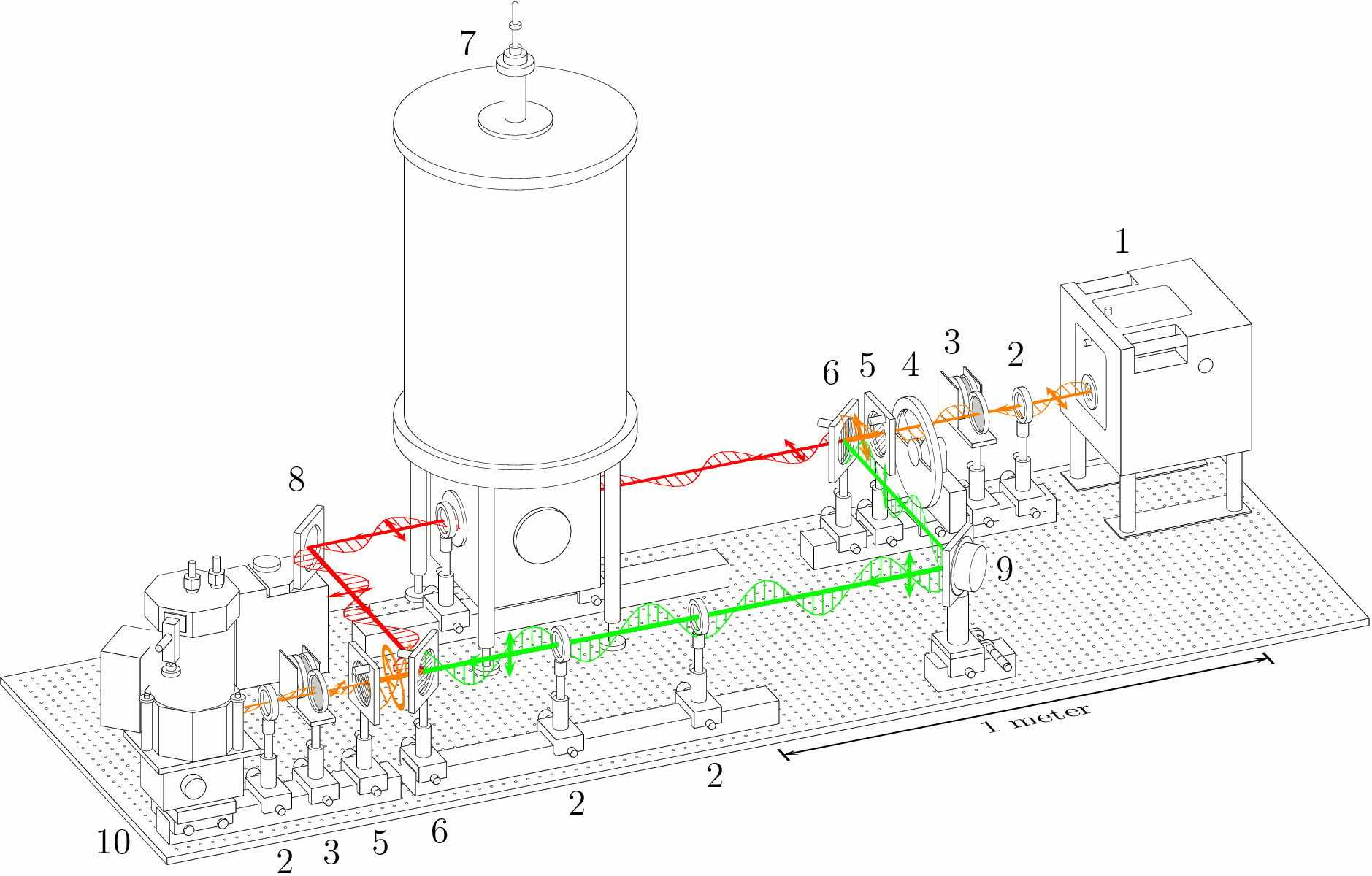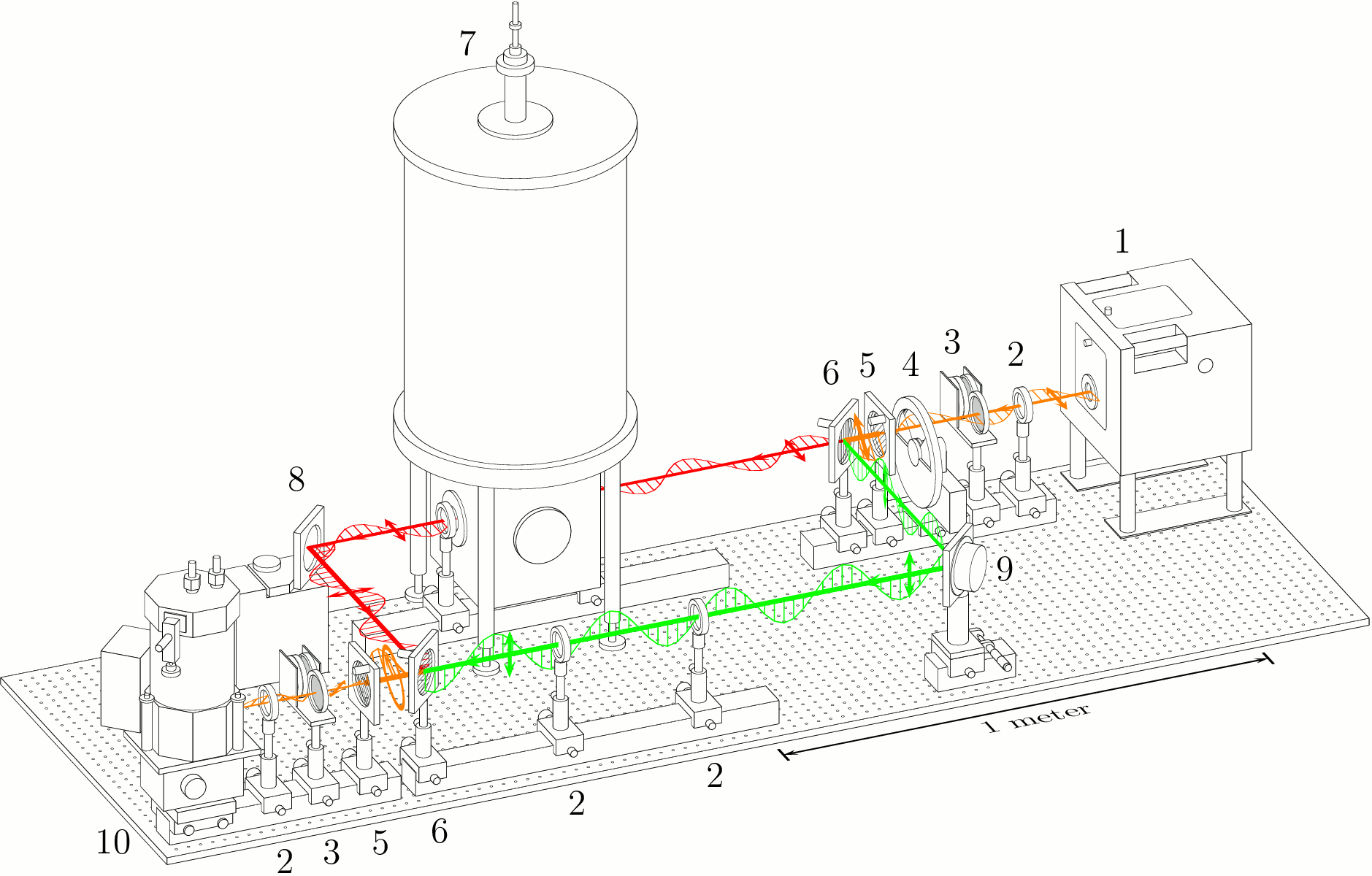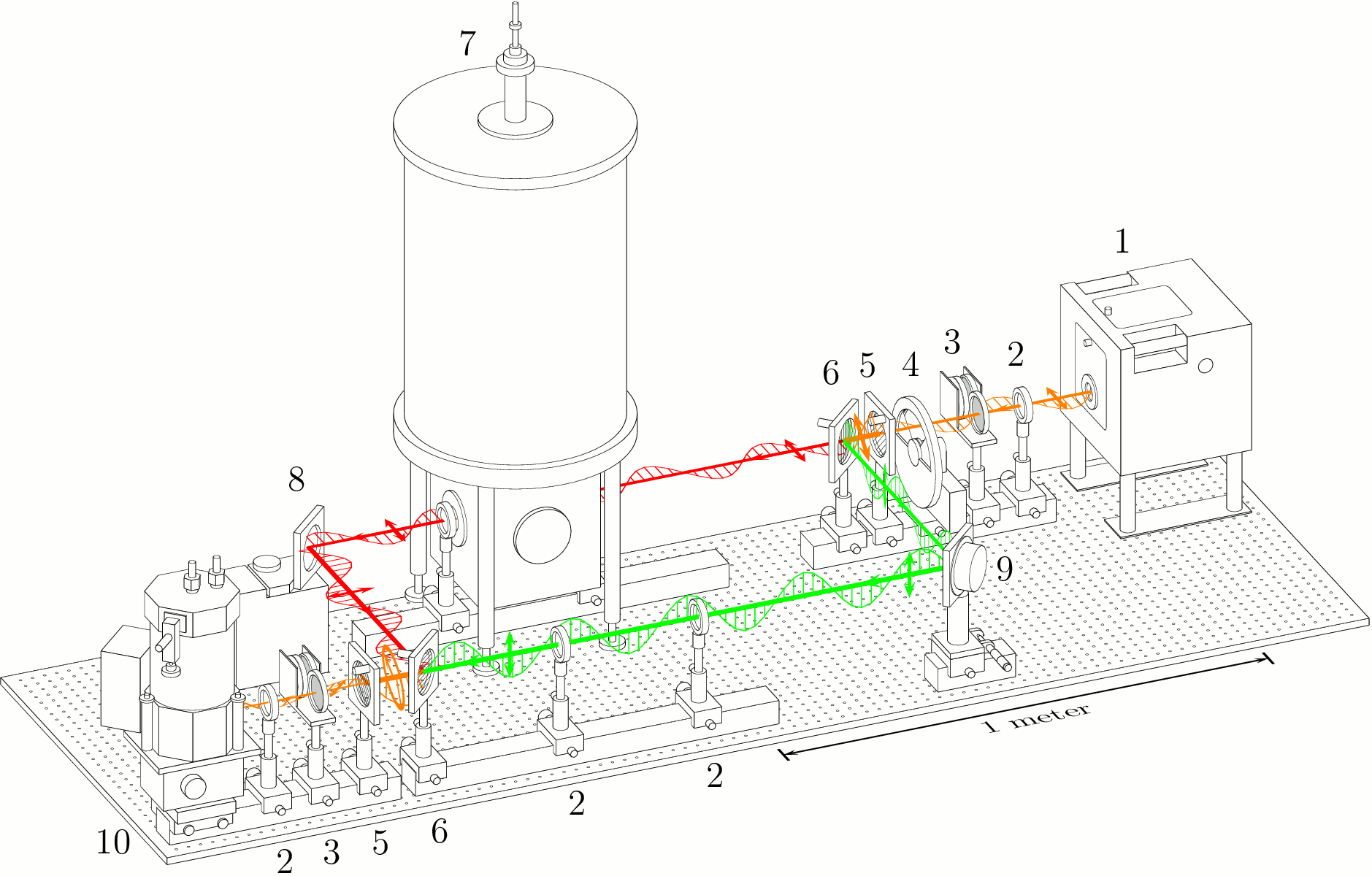
Scheme of a submillimeter Mach-Zender interferometer. The main arm with the sample
is in the upper left of the scheme (red rays), while the reference arm is shown
in the right bottom by the green rays. Short arrows indicate the polarization of the beams.
1 - backward wave oscillator (BWO), 2 - lenses, 3 - attenuators, 4 - chopper, 5 - wire grid polarizers,
6 - wire grid beam splitters, 7 - Oxfort cryomagnet, 8 - movable mirror, 9 - oscillating mirror (phae modulator),
10 - bolometer.
In the infrared and optical frequency ranges (1Thz < ν < 1000THz)
a Fourier-Transform technique is utilized and the reflectance is the basic property which is obtained in experiment.
Within this technique instead of spectral scan a measurement of the broadband source is
carried out as a function of phase shift (δ,x) between the halves of the beam (see figures).
The inverse Fourier-Transform of the measured signal corresponds directly to the frequency
spectrum of interest. To get the optical parameters the Kramers-Kronig
transformation has to be applied to the spectra. The combination with the
transmittance data from the terahertz range substantially improves the
accuracy of the Kramers-Kronig transformation.
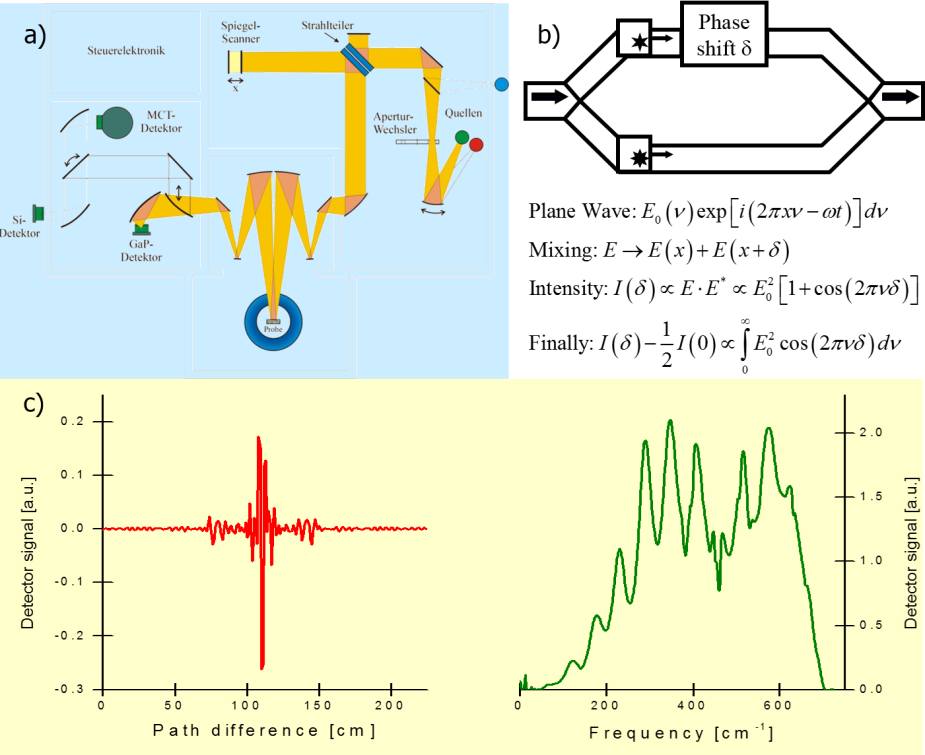
Fig. a) Scheme of the Fourier-Transform Spectrometer. [F.Mayr], b) Principle of the Fourier-Transform measurement, c) Typical measured signal (Interferogramm, left) and the fourier-transformed spectrum (right). [F. Mayr]

