Metamaterials and Photonic Crystals
 Negative refraction - may lead to surprising effects!
Metamaterials (artificial materials) can exhibit electromagnetic characteristics
unlike those of any conventional materials. Negative refraction and artificial
magnetism are some examples of properties that can be obtained and
controlled in these materials.
Negative refraction - may lead to surprising effects!
Metamaterials (artificial materials) can exhibit electromagnetic characteristics
unlike those of any conventional materials. Negative refraction and artificial
magnetism are some examples of properties that can be obtained and
controlled in these materials.
In general, metamaterials are supposed to have the characteristic
length scale of constituting elements much smaller than the radiation
wavelength. They therefore can in good approximation be considered as
continuous media with some effective electrodynamic properties.
Photonic crystals are strictly periodic structures with periods similar
to the wavelength. This similarity leads to some unusual effects like
waveguiding of light, anomalous refraction etc.
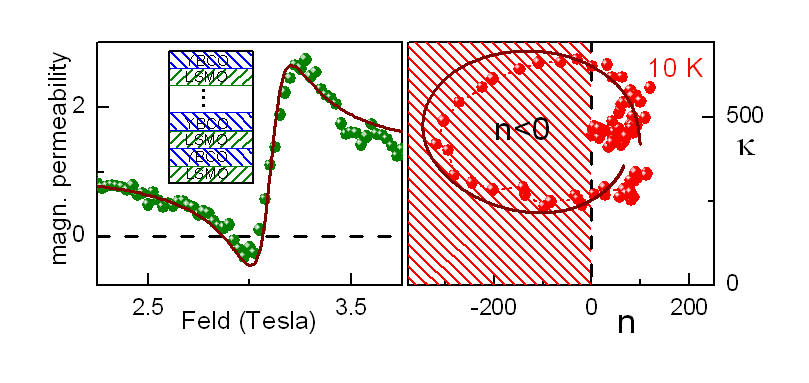
Negative refraction in Ferromagnet / Superconductor superlattices
According to the basic idea a material with sumultaneously negative dielectric
permittivity and magnetic permeabilily would reveal negative refraction, i.e.
negative phase velocity. In agreement with this idea the superlattices
ferromagnet/superconductor YBCO/LSMO would reveal negative refraction.
In these systems the superconducting YBa2Cu2O7
layers are responsible for the negative dielectric permittivity. The
ferromagnetic (La:Sr)MnO3 provide negative magnetic
permeability close to the resonance (left panel). With both conditions fulfilled
the negative refractive index is realized (right panel,
Phys. Rev. Lett. 95, 247009 (2005)).
More rigorous calculations show that weaker conditions for the negative
refraction can be realized. In case of metals negative magnetic
permeability is a sufficient condition for negative refractive index.
In this sence all ferromagnetic metals may reveal negative refraction
close to the ferromagnetic resonance. Recently we could prove this
condition for Iron and Cobalt.
|
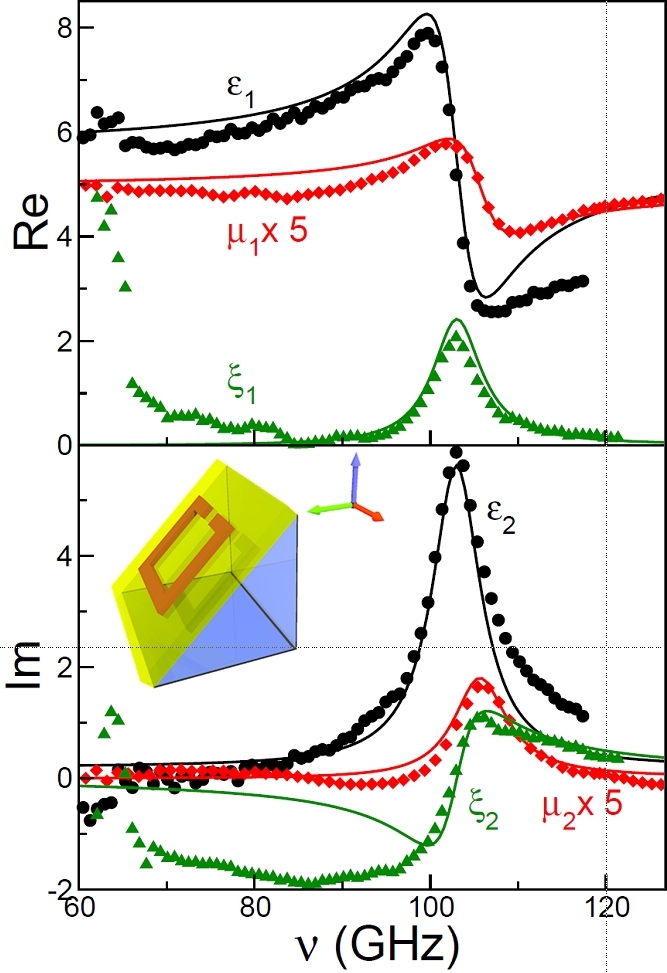
Metamaterials as perfect magnetoelectrics
Perfect magnetoelectrics are materials in which magnetoelectric susceptibility equals the geometric average of electric and magnetic susceptibilities (χme)2 = χeχm. Conventional magnetoelectrics show the values of χme far below the theoretically allowed. Recently we could show that the metamaterials made of split ring resonators can indeed reach the perfect value of the magnetoelectric susceptibility [arXiv:1004.4524]. |
Selected publications
-
S. Engelbrecht, A. M. Shuvaev, Y. Luo, V. Moshnyaga, and A. Pimenov
Negative refraction in natural ferromagnetic metals
arXiv:1011.3663 -
S. Engelbrecht, M. Wunderlich, A. M. Shuvaev, and A. Pimenov
Colossal optical activity of split-ring resonator arrays for millimeter waves
Appl. Phys. Lett. 97, 081116 (2010) -
A. M. Shuvaev, S. Engelbrecht, M. Wunderlich, A. Schneider, and A. Pimenov
Metamaterials proposed as perfect magnetoelectrics
arXiv:1004.4524 -
A. Schneider, A. Shuvaev, S. Engelbrecht, S. O. Demokritov, and A. Pimenov
Electrically Excited Inverse Electron-Spin-Resonance
Phys. Rev. Lett. 103, 103907 (2009)
-
A. Pimenov, K. Gehrke, V. Moschnyaga, K. Samwer, and A. Loidl
Negative Refraction in a Metallic Ferromagnet
Phys. Rev. Lett. 98, 197401 (2007) -
A. Pimenov and A. Loidl
Experimental demonstration of artificial dielectrics with a high index of refraction
Phys. Rev. B 74, 193102 (2006) -
A. Pimenov and A. Loidl
Negative Brechung in Ferromagnet-Supraleiter-Multilagen
Physik in unserer Zeit 37, 112 (2006) -
A. Pimenov and A. Loidl
Dynamic conductivity and permittivity in metallic photonic crystals
Phys. Rev. Lett. 96, 063903 (2006) -
A. Pimenov, A. Loidl, P. P. Przyslupski, and B. Dabrowski
Negative refraction in ferromagnet/super-conductor superlattices
Phys. Rev. Lett. 95, 247009 (2005)
-
A. Pimenov and A. Loidl
Focusing of light beyond the Abbe barrier
Appl. Phys. Lett. 83, 4122 (2003)

