Many-Body Quantum Field Theory (copy 1)
Strongly correlated electron systems show the arguably most fascinating and at the same time the least understood physical phenomena in solid state physics, such as high-temperature superconductivity as in the cuprates, the Mott metal-insulator transition in VO
, or the physics of quantum critical points in heavy fermion compounds. Unfortunately, from the theoretical perspective, these systems elude any ab initio description by density functional theory due to the intrinsic mean-field nature of the latter approach. This calls for the development of advanced quantum field theory (QFT) many-body methods capable of treating electronic correlations non-perturbatively, which represents one of the central research areas of our group.
Modeling correlated electron systems
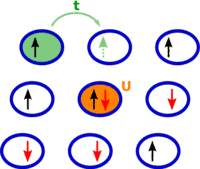
The most basic model, in some sense the “Drosophila” of correlated lattice electrons, is the Hubbard model (see Fig. 1), described by the following Hamiltonian:
The first term (kinetic energy) describes the hopping of an electron with spin from lattice site
to lattice site
, while the second term (potential energy) accounts for the strong Coulomb repulsion
between two electrons at the same lattice site, which is responsible for the correlations in the system. The Green's functions are the essential objects for a QFT description of a correlated system since they are experimentally accessible. However, despite the apparent simplicity of Hamiltonian (1), the Green's function for the Hubbard model cannot be calculated exactly. Hence, the development of approximations, adopting advanced techniques of QFT, is at the frontier of research in theoretical solid state physics.
Beyond dynamical mean field theory (DMFT)
Over the last twenty years DMFT has emerged as the standard tool for calculating the Green’s functions of strongly correlated systems, described by the Hubbard Hamiltonian (1) and related models. Within DMFT, the actual lattice problem is replaced by only one interacting lattice site, which hybridizes with a self-consistently determined non-interacting bath (see Fig. 2).
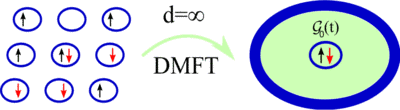
This way one includes local correlation effects non-perturbatively but neglects nonlocal spatial correlations. In this respect, DMFT works quite well for systems with a large number of neighboring sites (high coordination number) or at high temperatures. However, it fails to capture the correct physics in situations where nonlocal correlations become crucial. This is the case, e.g., for systems in the vicinity of a second-order phase transition, where one observes fluctuations on all length scales and a diverging correlation length. For an appropriate description of this important class of phase transitions one has to include nonlocal correlation effects on all length scales on top of the local ones of DMFT. This can be achieved by (Feynman) diagrammatic extensions of DMFT. Their basic idea is to construct nonlocal Feynman diagrams for the (irreducible) Green’s functions with the nonlocal DMFT Green’s function and the local DMFT
-particle vertex functions
(see Fig. 3).
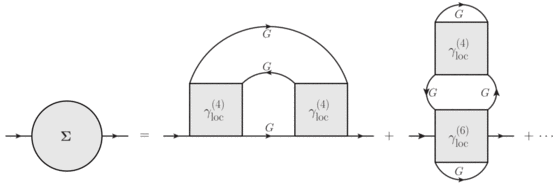
It turns out that the description of second-order phase transitions requires an infinite (ladder) resummation of such diagrams. In order to perform such resummations in a systematic way, different methods are currently under consideration in our group:
Dynamical vertex approximation (D?A)
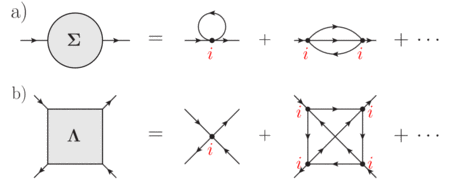
This approach is based on the local fully irreducible vertex
. Its basic idea is to raise the DMFT assumption of locality of the fully irreducible one-particle vertex (i.e., the self-energy, see Fig. 4a) to the two-particle level. This means that D
A assumes the locality of the fully irreducible two-particle vertex function
(see Fig. 4b). Starting from this local
, the parquet and the Bethe-Salpeter equations allow for a systematic resummation of nonlocal ladder diagrams, capturing in this way the physics of second-order phase transitions and leading to nonlocal corrections of the local DMFT self-energy.
One-particle irreducible approach (1PI)
This approach is based on the functional integral representation of the Green’s functions and on the generating functional formalism. Its basic idea is to decouple local and nonlocal degrees of freedom of the Hubbard model by means of a Hubbard-Stratonovich transformation and to apply a Legendre transformation to the local part in order to obtain a one-particle irreducible theory. By being one-particle irreducible, it avoids the spurious reducible self-energy diagrams of the standard approximation employed in the dual fermion theory.
Outlook
In order to go beyond the model level and describe real correlated materials, it is necessary to combine the above-mentioned approaches with ab initio methods (e.g., LDA). In this respect, the understanding of unconventional superconductivity, quantum criticality or weak localization (on the model level) as well as the application of DA to real materials are the aim of the ERC project AbinitioD?A. Ab initio D
A includes the full Coulomb interaction
instead of the Hubbard
as lowest-order contribution to the fully irreducible vertex
, this way allowing for the description of local and nonlocal correlation effects in real materials.
Further reading:
[1] A. Toschi, A. A. Katanin, and K. Held, Phys. Rev. B 75, 045118 (2007)
[2] A. A. Katanin, A. Toschi, and K. Held, Phys. Rev. B 80, 075104 (2009)
[3] G. Rohringer, A. Toschi, A. A. Katanin, and K. Held, Phys. Rev. Lett. 107, 256402 (2011)
[4] A. Toschi, G. Rohringer, A. A. Katanin, and K. Held, Annalen der Physik 523, 698 (2011)
[5] G. Rohringer, A. Toschi, H. Hafermann, K. Held, V. I. Anisimov, and A. A. Katanin, Phys. Rev. B 88, 115112 (2013)

